Crank-Nicolson and Projected SOR for pricing american options

1 minute read

In this post I have elaborated on using Crank-Nicolson method to price a european option. It is more complicated to price american options using this method because they can be exercised any time before expiration time. To employ Crank-Nicolson for american options, linear systems in each layer can be solved using a numerical method called Projected SOR (Successive Overrelaxation). Using this method, for each time layer i, we have the iterative scheme:

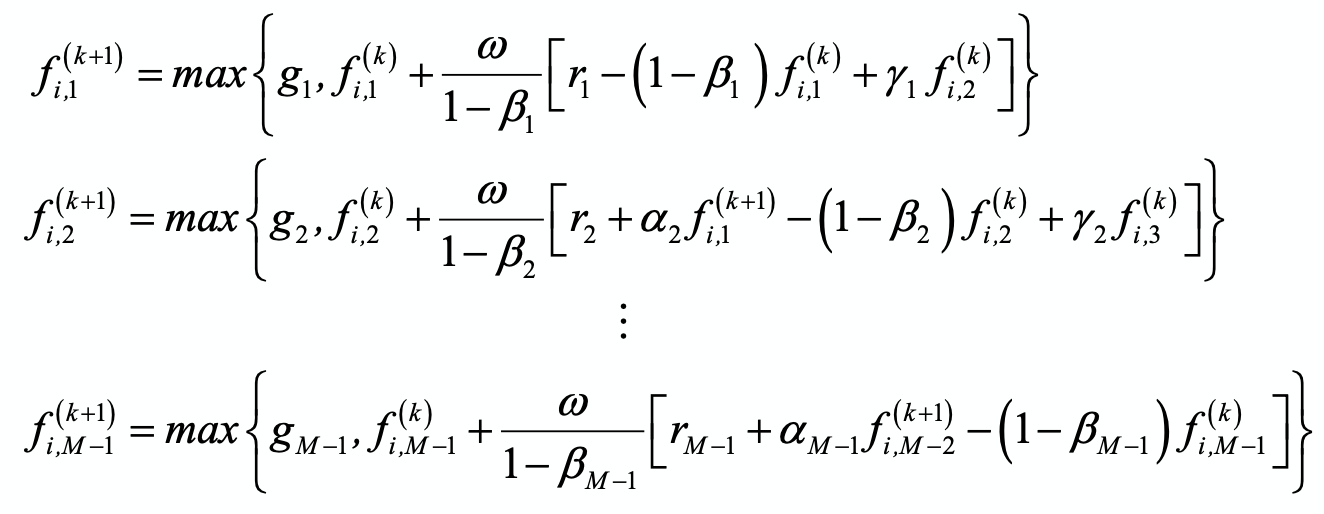
center

Pyhon implementation

Suppose we have an american put option:

import numpy as np

T = 5/12
S_0 = 50
K = 50
sigma = 0.4
r = 0.1
price = 0

tol = 0.001
omega = 1.2

S_max = 100

N = 250
M = 100
dt = T / N
ds = S_max / M

I = np.arange(0, M+1)
J = np.arange(0, N+1)

old_val = np.zeros(M-1)
new_val = np.zeros(M-1)

# Boundary and final conditions
payoff = np.maximum(K - I[1:M] * ds, 0)
old_layer = payoff
bound_val = K * np.exp(-r * (N - J) * dt)

# Calculating elements of M
alpha = 0.25 * dt * (sigma**2 * (I**2) - r * I)
alpha = alpha[1:]
beta = -dt * 0.5 * (sigma**2 * (I**2) + r)
beta = beta[1:]
gamma = 0.25 * dt * (sigma**2 * (I**2) + r * I)
gamma = gamma[1:]

M2 = np.diag(1+beta[:M-1]) + np.diag(alpha[1:M-1], k=-1) + np.diag(gamma[:M-2], k=1)
b = np.zeros(M-1)

for j in range(N-1, -1, -1):
    b[0] = alpha[0] * (bound_val[j] + bound_val[j+1])
    rhs = M2 @ old_layer + b
    old_val = old_layer
    error = 1000000
    while error > tol:
        new_val[0] = np.maximum(payoff[0], old_val[0] + (omega/(1-beta[0]))*(rhs[0] - (1-beta[0])*old_val[0] + gamma[0] * old_val[1]))
        for k in range(1, M-2):
            new_val[k] = np.maximum(payoff[k], old_val[k] + (omega / (1 - beta[k])) * (
                        rhs[k] - (1 - beta[k]) * old_val[k] + alpha[k] * new_val[k-1] + gamma[k] * old_val[k+1]))
        new_val[M-2] = np.maximum(payoff[M-2], old_val[M-2] + (omega / (1 - beta[M-2])) * (
                rhs[M-2] - (1 - beta[M-2]) * old_val[M-2] + alpha[M-2] * new_val[M-3]))
        error = np.linalg.norm(new_val - old_val)
        old_val = new_val
    old_layer = new_val


prices_t0 = np.concatenate(([bound_val[0]], old_layer, [0]))
idown = int(np.floor(S_0 / ds))
iup = int(np.ceil(S_0 / ds))
print(idown)
print(iup)
if idown == iup:
    price = prices_t0[idown]
else:
    price = prices_t0[idown] + ((iup - (S_0 / ds)) / (iup - idown)) * (prices_t0[iup] - prices_t0[idown])

print(price)

50
50
4.367132414514241

You May Also Enjoy