A smart implementation of binomial lattice method

In this post I introduce the memory and CPU-efficient way of implementing binomial lattice method for option pricing. In this way you should note this pattern of values on binomial tree:

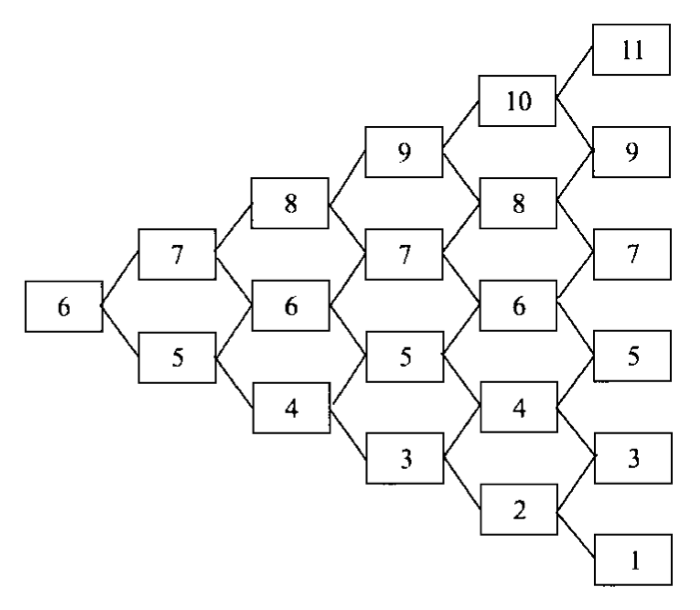
Python implementation

# Implements for a european put option
import numpy as np

S_0 = 50
K = 50
sigma = 0.4
r = 0.10
T = 5/12
M = 5
dt = T / M

u = np.exp(sigma * np.sqrt(dt))
d = 1 / u

p = (np.exp(r * dt) - d) / (u - d)

discount = np.exp(-r * dt)

p_u = discount * p
p_d = discount * (1-p)

SVals = np.zeros(2*M+1)
PVals = np.zeros(2*M+1)

SVals[0] = S_0 * d**M

for i in range(1,2*M+1):
    SVals[i] = SVals[i-1] * u

for i in range(0, 2*M+1, 2):
    PVals[i] = np.maximum(K - SVals[i], 0)

for tau in range(0, M):
    for i in range(tau+1, 2*M+1-tau, 2):
        PVals[i] = p_u * PVals[i+1] + p_d * PVals[i-1]

print(PVals[M])

4.319018716515822